Prak-9: Transformasi Fourier

Imam Ibnu Badri Komputasi Teknik 08.53

Kompetensi dasar dan indikator

1 Kompetensi Dasar

Setelah mengikuti praktikum ini, mahasiswa mampu:

Memahami dan menganalisis sinyal menggunakan Transformasi Fourier menggu nakan Matlab.

2 Indikator

l. Memahami dan menganalisis sinyal menggunakan Transforrnasi Fourier dengan menggunakan Matlab.

Mahasiswa berhasil membuat sourcode untuk menganalisis sinyal menggunakan Transformasi Fourier menggunakan Matlab.

Dasar Teori

a. Transformasi Fourier
Transformasi Fourier adalah transformasi yang dapat merubah suatu sinyal dari domain waktu s(t) kedalam domain frekuensi S(f).

Tujuan dilakukanya transformasi ini adalah untuk mendapatkan informasi apakah suatu sinyal memiliki frekuensi tertentu atau tidak.

Transformasi Fourier menggabungkan sinyal ke bentuk fungsi eksponensial dari frekuensi yang berbeda-beda.

Persamaan transformasi Fourier ditunjukkan pada Persamaan 9.1.

b. Discrete Time Fourier Transformation (DTFT) dan Sampling Theorem Sampel sinyal domain waktu kontinyu diambil untuk mendapatkan urutan diskrit. Domain frekuensi yang sesuai bersifat periodik dengan periode frekuensi sampling F_s. Amplitudo domain frekuensi yang diperoleh dengan
sampling diskalakan oleh faktor F_s . Dalam hal ini domain waktu bersifat diskrit dan domain frekuensi bersifat kontinyu dan periodik. Persamaan DTFT ditunjukkan pada Persamaan 9.2 dan Persamaan 9.3.

c. Discrete Fourier Transformation (DFT)
Spektrum sampel diskrit (DTFT) bersifat periodik dengan frekuensi sampling F_s . DPT diperoleh dengan sampling DTFT untuk satu periode. Jumlah sampel diperoleh dari satu periode domain frekuensi DTFT yang ditunjukkan pada Persamaaan 9.4.

d. Fast Fourier Transform (FFT)

Jumlah perhitung DFT dikurangi oleh algoritma fast Fourier transform. Persamaan matematis fast Fourier transform ditunjukkan pada Persamaan 9.5.

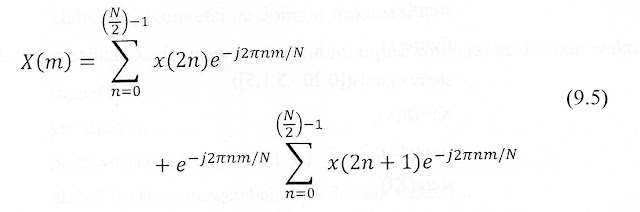
e. Inverse Fourier Transform
Transformasi Fourier adalah generalisasi dari deret Fourier kompleks yang dibatasi oleh L→ ∞. Untuk menentukan inverse Fourier Transform ditunjukkan pada Persamaan 9.6.

Langkah Praktikum

Konversi Sederhana Pada Sinyal Dasar
A. Pembangkitan sinyal sinus dalam domain waktu dan domain frekuensi

1) Anda buat sebuah program pembangkitan sinyal sinus dalam domain waktu dan domain frekuensi seperti berikut :

clc
t=0:.001:2;
x_t=sin(2*pi*t);
figure(1);
plot(x_t);axis([0 2010 -1.2 1.2])
X_F=fft(x_t);
figure(2);
plot(abs(X_F));axis([-100 2100 -10 1100])

2) Tambahkan perintah berikut ini untuk mengkonversikan kembali dari domain frekuensi ke dalam domain waktu.

x_tt=ifft(X_F);
figure(3);
plot(x_tt);axis([0 2010 -1.2 1.2])

3) Anda buat sebuah program pembangkitan sinyal persegi dalam domain waktu diskrit dan domain frekuensi seperti berikut :

x=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0]
stem(x)
figure(1);
stem(x);axis([0 20 -.5 1.5])
Xf=fft(x);
figure(2);
stem(Xf)
stem(abs(Xf));axis([0 20 -.5 5.5])
figure(3);
xtt=ifft(Xf);
stem(xtt);axis([0 20 -.5 1.5])

4) Tambahkan perintah berikut ini untuk mengkonversikan kembali dari domain frekuensi ke dalam domain waktu.

figure(3);
xtt=ifft(Xf);
stem(xtt);axis([0 20 -.5 1.5])

B. Pembangkitan sinyal persegi
1) Buat program baru untuk pembangkitan sinyal persegi dengan cara seperti berikut

clc
Fs=10000;
t=0:1/Fs:.0625;
y=square(2*pi*30*t);
figure(1);
plot(t,y);axis([0 0.07 -1.5 1.5])
xlabel('(a)Sinyal input kotak');
Yf=fft(y);
Yf_dB=20*log10(abs(Yf));
figure(2);
f=1:(length(Yf)/2);
Yf_dBx=Yf_dB(1:length(Yf)/2);
plot(0.5*Fs*(f/length(Yf)),Yf_dBx);
xlabel('(b)Konversi ke domain frekuensi');

2) Tambahkan kode program berikut ini untuk konversi ke domain waktu .

figure(3)
ytt=ifft(Yf);
plot(t,ytt);axis([0 0.07 -1.5 1.5])
xlabel('(c)Hasil Pengembalian ke domain waktu');

Latihan

Gunakan Matlab dalam menyelesaikan soal-soal berikut :
1. Tentukan deret Fourier dari

2 Tentukan deret Fourier dari

3. Carilah transformasi Fourier dari bentuk gelombang pulsa di bawah ini

4. Cailah transformasi Fourier dari

5. Tentukan inverse Fourier transform dari fungsi berikut ini

Jawab

Latihan Kampus

Latihan1 - Membangkitkan sinyal sinus dan mengubah dalam domain frekuensi

clc
subplot(2,1,1);
t=0:.001:2;
x_t=sin(2*pi*t);
%figure(l);
plot(x_t);
axis([0 2010 -1.2 1.2])

subplot(2,1,2);
X_F=fft(x_t);
%figure(2);
plot(abs(X_F))
axis([-100 2100 -10 1100]);

Output

Latihan2 - Membangkitkan sinyal diskrit dan mengubah dalam domain frekuensi

clc
subplot(3,1,1);
t=0:.001:2;
x_t=sin(2*pi*t);
%figure(l);
plot(x_t);
axis([0 2010 -1.2 1.2])

subplot(3,1,2);
X_F=fft(x_t);
%figure(2);
plot(abs(X_F))
axis([-100 2100 -10 1100]);

subplot(3,1,3);
x_tt=ifft(X_F);
plot(x_tt)
axis([0 2010 -1.2 1.2]);

output

Latihan3 - Membangkitkan sinyal persegi, mengubah dalam domain frekuensi dan mengubah kembali ke domain waktu

subplot(3,1,1);
x=[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0]
stem(x)
title('Sinyal Persegi Dalam Domain Waktu Diskrit');
axis([0 20 -.5 1.5])

subplot(3,1,2);
Xf=fft(x);
stem(abs(Xf));
title('Hasil FFT Sinyal Persegi ke Dalam Domain Frekuensi Diskrit');
axis([0 20 -.5 5.5])

subplot(3,1,3);
xtt=ifft(Xf);
stem(xtt);
title('Hasil Invers FFT Sinyal Persegi ke Dalam Domain Waktu Diskrit');
axis([0 20 -.5 1.5])

Output

Latihan1

figure(3) ytt=ifft(Yf);
plot(t,ytt) ;axis([O 0.07 -1.5 1.5))
xlabel('(c) Hasil pengembalian ke domain waktu');

Latihan1

figure(3) ytt=ifft(Yf);
plot(t,ytt) ;axis([O 0.07 -1.5 1.5))
xlabel('(c) Hasil pengembalian ke domain waktu');

Latihan1

figure(3) ytt=ifft(Yf);
plot(t,ytt) ;axis([O 0.07 -1.5 1.5))
xlabel('(c) Hasil pengembalian ke domain waktu');

Latihan 4 Membangkitkan

clc;
Fs=10000;
t=0:1/Fs:0.0625;
y=square(2*pi*30*t);

subplot(3,1,1);
plot(t,y);
axis([0 0.07 -1.5 1.5]);
xlabel('(a) Sinyal Input Kotak');
Yf=fft(y);
Yf_dB=20*log10(abs(Yf));

subplot(3,1,2);
f=1:(length(Yf)/2);
Yf_dBx=Yf_dB(1:length(Yf)/2);
plot(0.5*Fs*(f/length(Yf)),Yf_dBx);
xlabel('(b) Konversi ke domain frekeunsi');
Yf=fft(y);
Yf_dB=20*log10(abs(Yf));

subplot(3,1,3);
ytt=ifft(Yf);
plot(t,ytt);axis([0 0.07 -1.5 1.5])
xlabel('(c) Hasil pengembalian ke domain waktu');
Yf=fft(y);
Yf_dB=20*log10(abs(Yf));

Output