Prak-11: Transfomasi Z

Imam Ibnu Badri       Komputasi Teknik    08.56

Kompetensi dasar dan indikator

1 Kompetensi Dasar

---

Setelah mengikuti praktikum ini, mahasiswa mampu:

• Memahami dan menganalisis sinyal menggunakan Transformasi Z menggunakan Matlab.

2 Indikator

---

1. Memahami dan menganalisis sinyal menggunakan Transformasi Z dengan menggunakan Matlab .

• Mahasiswa berhasil membuat sourcode untuk menganal isis sinyal menggunakan Transformasi Z menggunakan Matlab.

Dasar Teori

a. Z-Transform
Persamaan matematis z-transform ditunjukkan pada Persamaan 11.1



Untuk menentukan z-transform pada Matlab dengan mengetik perintah berikut

 >> syms n
 >> f = sin(n);
 >> ztrans(f)

output



b. Inverse Z-Transform
Persamaan matematis inverse z-transform ditunjukkan pada Persamaan 11.2



Untuk menentukan inverse z-transform pada Matlab dengan mengetik perintah berikut

 >> syms z
 >> f = 2*z/(z-2)^2;
 >> iztrans(f)

output:

Langkah Praktikum

1. Mulailah menghitung ekspansi parsial dari fungsi transfer bentuk z berikut ini.





Ekpresikan fungsi trsnfer-z di dalam bentuk pangkat z-1 berikut ini





2. Buatlah program pada Matlab untuk menentukan bentuk ekspansi pecah parsial seperti dibawah ini.

 B=[0;6;34;0];                   %koef. numerator N(z)
 A=[1;-7;31;-25];              %koef. denominator D(z)
 [R,P,K]=residuez(B,A)    %Hitung partial fraction expansion

3. Cobalah lihat nilai-nilai R, P dan K dari perintah diatas, apakah nilainya seperti berikut ini

Latihan

1. Tentukan inverse z -transform dari fungsi berikut ini


A.

 syms z
 F = (z*(2*z-1))/((z-1)*(z+0.5));
 iztrans(F)

B.

 syms z
 F = 1/((z-1)*(z+0.5));
 iztrans(F)

C.

 syms z
 F = 9/((z-1)*(z+0.5)^2);
 iztrans(F)

D.

 syms z
 F = ((5*z)*(z-1))/(z^2-1.6*z+0.8);
 iztrans(F)

Output



2. Tentukan z-transform dari fungsi berikut ini

Jawab

1.

 syms z
 F=(z*(2*z-1))/((z-1)*(z+0.5));
 iztrans(F)

output

Catatan Kuliah

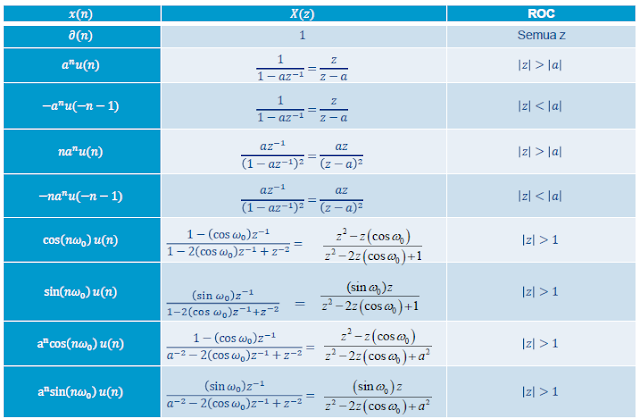
latihan 1

 syms n a
 x =a^n;
 z=ztrans(x)

latihan 2

 syms n a
 x = -a^n;
 z=ztrans(x)

latihan 3

syms n a
x = n*a^n;
z=ztrans(x)

latihan 4

 syms n a
 x = -n*a^n;
 z=ztrans(x)

Latihan 5

 syms n w
 x = cos(n*w);
 z=ztrans(x)

Latihan 6

 syms n w
 x = sin(n*w);
 z=ztrans(x)

Latihan 7

 syms a n w
 x = (a^n) *cos(n*w);
 z=ztrans(x)

Latihan 8

 syms a n w
 x = (a^n) *sin(n*w);
 z=ztrans(x)

keterangan
un menyatakan posisi atau menandakan mulai , tidak dimakukan dalam rumus
u(n) berarti mulai dari posisi
-u -1 berartimulai dari 1


Link:
https://www.coursehero.com/file/47708655/009-transformasi-Zpdf/
https://yulisun.staff.telkomuniversity.ac.id/files/2016/06/009_transformasi-Z.pdf

NB :
Download laporan di Halaman Daftar Isi

Daftar Isi - Teknik Komputasi